A Causality Summary Part I – Igor L.R. Azevedo

Main Reference: https://arxiv.org/abs/2405.08793

Have you ever thought about the word “causal” in the sentence we’ve all heard: “Smoking causes lung cancer”?

It sounds pretty simple, right? The way I see it, at least, is the following: if someone has lung cancer and they smoke, we assume smoking caused it.

smoke --- causes ---> cancer

Okay, but what about the many other possibilities for the cancer to have happened? For example, genetic mutations, alcohol consumption, aging, unhealthy lifestyle, radiation exposure, etc all cause cancer.

Let’s imagine the scenario in which we’re analyzing an 80-year-old man who has smoked since he was 21. In addition, every time he smoked at night, he would always have at least three cans of beer, and he worked throughout the day on a farm, being exposed to the sunlight for 8 hours a day, and he was obese by the time he was diagnosed with lung cancer.

How can we precisely tell that the cigarettes were responsible for this? Don’t get me wrong; I’m not a denier that cigarettes are not good for our health, but this question is fascinating. How can we isolate all those other variables to say that if he had not smoked, his chances of having lung cancer would be smaller?

It is thus an important, if not the most important, job for practitioners of causal inference to convincingly argue why some variables are included and other were omitted. They also must argue why some of the included variables are considered potential causes and why they chose a particular variable as an outcome. This process can be thought of as defininig a small universe in which causal inference must be performed.

Probabilistic Graphical Models

A probabilistic graphical model, also referred to as a Bayesian graphical model, is a directed graph $G = (V, E)$ , where $V$ is a set of vertices and $E$ is a set of directed edges. Each node $v \in V$ corresponds to a random variable, and each edge $e = (v_s, v_e)$ represents the dependence of $v_e$ on $v_s$ .

For each node $v \in V$ , we define a probability distribution $p_v(v | pa(v))$ over this variable conditioned on all the parent nodes

$pa(v) = \{ v' \in V | (v', v) \in E \}$

At first, when I looked at this equation, I didn’t completely understand it. Let’s break into parts

1. Node $v \in V$ : Here, $v$ represents a node, and $V$ is the set of all nodes in a graph. This means $v$ is an individual node that belongs to the set of nodes, $V$ .

2. Probability distribution $p_v(v | pa(v))$ : This represents a conditional probability distribution for node $v$ given its parent nodes $pa(v)$ . Essentially, it’s saying that the value or state of node $v$ is influenced by its parent nodes, and this distribution captures how $v$ depends on them.

3. Parent nodes $pa(v)$ : The function $pa(v)$ refers to the set of parent nodes of $v$ . In other words, $pa(v)$ represents all the graph nodes with a directed edge pointing to $v$ . These parent nodes directly influence the state of node $v$ .

4. Set notation $pa(v) = \{ v'\in V \mid (v', v) \in E \}$ : This equation defines the set of parent nodes. It means that $pa(v)$ is the set of nodes $v'$ that are in $V$ (the set of all nodes), where there exists an edge $(v', v) \in E$ . In graph terminology, $E$ is the set of edges, and $(v', v)$ indicates an edge going from node $v'$ to node $v$ . This implies that $v'$ is a parent of $v$ .

In summary:

$v$ is a node in a graph.
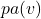$pa(v)$ is the set of parent nodes for $v$ (i.e., nodes that have edges leading to $v$ ).
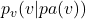$p_v(v | pa(v))$ is the probability of $v$ conditioned on its parents.
The set definition 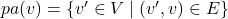$pa(v) = \{ v' \in V \mid (v', v) \in E \}$ means that 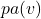$pa(v)$ consists of all nodes 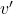$v'$ that have directed edges to $v$ .

We can then write a joint distribution over all the variables as

$p_V = \prod_{v \in V}p_v(v | pa(v))$

With $P$ , a set of all conditional probabilities $p_v$ ‘s, we can denote any probabilistic graphical model as a triplet $(V, E, P)$

1. Joint Distribution $p_V$ :

The equation represents the joint probability distribution over all nodes in the graph.
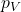$p_V$ denotes the graph’s joint probability distribution for all the nodes (variables). This is the overall probability of observing a configuration of all the variables.

2. Set of Nodes $V$ :

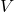$V$ represents the set of all graph nodes (or variables). Each node 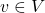$v \in V$ is an individual variable whose value depends on the values of its parent nodes.

3. Conditional Probability $p_v(v | pa(v))$ :

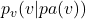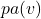$p_v(v | pa(v))$ is the conditional probability of node $v$ given its parent nodes $pa(v)$ . This expresses how the state of node $v$ depends on the states of its parents in the graph.
It indicates that the value of $v$ is not independent but influenced by its parents (nodes that have directed edges pointing to $v$ ).

4. Parent Nodes $pa(v)$ :

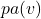$pa(v)$ refers to the set of parent nodes for a node $v$ . These are the nodes that have a directed edge pointing to $v$ . In other words, the state of node $v$ is influenced by the states of these parent nodes.
Specifically, 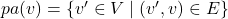is a formal definition of the parent set. Here:
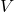- $V$ is the set of all nodes in the graph.
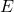- $E$ is the set of edges in the graph.
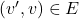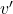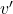- The expression $(v', v) \in E$ means a directed edge from node $v'$ to node $v$ , indicating that $v'$ is a parent of $v$ .

5. Overall Meaning:

The product 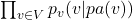$\prod_{v \in V} p_v(v | pa(v))$ is a way of expressing the joint distribution of all the variables in the graph.
It says that the joint probability of all nodes can be computed by multiplying the individual conditional probabilities of each node given its parents.
The idea is that the graph structure encodes dependencies between the variables. The joint distribution is factorized in terms of these conditional dependencies, reflecting the local structure of the graph.

From the joint distribution, we can derive conditional distributions for various subsets of the variables by marginalizing the variables that we are not interested in. Marginalization involves summing out the unwanted variables, and conditional probability is used to express the relationship between the remaining variables.

Step 1: Marginalizing a Variable

Let’s say we are not interested in a particular node $\bar{v} \in V$ in the graph. To marginalize over this variable, we sum out $\bar{v}$ from the joint distribution $p_V(V)$ . This means we consider the total probability of the other variables while ignoring $\bar{v}$ . The result is:

$p(V \backslash \{ \bar{v} \}) = \sum_{\bar{v}} p_V(V)$

Here:

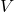$V$ represents the entire set of variables.
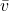$\bar{v}$ is a specific value we are conditioning on.
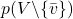$p(V \backslash \{ \bar{v} \})$ is the marginal probability distribution over all variables except $\bar{v}$ .
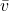The summation over 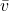$\bar{v}$ indicates that we are summing out the variable $\bar{v}$ .

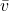Note: when we say “we are summing out the variable $\bar{v}$ “, we are note “excluding its value” in the sense of ignoring it or discarding it enterily. Instead, summing out $\bar{v}$ means that we are eliminating the dependency on $\bar{v}$ by summing over all possible values that $\bar{v}$ can take. This process integrates out (for continous variables) or sums out (for discrete variables) the variable from the joint distribution.

This step reduces the joint distribution to the marginalized distribution over the remaining variables.

Step 2: Turning Joint Probability into Conditional Probability

We can also express a conditional probability by using the definition of conditional probability. Remember,

$p(A | B) = \frac{p(A, B)}{p(B)}$

To condition on a specific variable, say $\tilde{v}$ , we divide the joint probability by the marginal probability of $\tilde{v}$ . The conditional probability of the remaining variables, given $\tilde{v}$ , is:

$p(V \backslash \{ \tilde{v} \} | \tilde{v}) = \frac{p_V(V)}{p_{\tilde{v}}(\tilde{v})}$

Here:

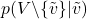$p(V \backslash \{ \tilde{v} \} | \tilde{v})$ represents the conditional probability of all the remaining variables in 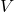$V$ given that 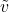$\tilde{v}$ takes some specific value.
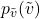$p_{\tilde{v}}(\tilde{v})$ is the marginal probability of $\tilde{v}$ .

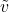This equation shows how to convert the joint distribution into a conditional distribution by normalizing with the marginal probability of $\tilde{v}$ .

Step 3: Marginalizing with Conditional Probability

Now, we can combine marginalization and conditional probability to express the marginalized probability explicitly using the definition of conditional probability.

First, let’s express the marginal probability $p(V \backslash \{ \bar{v} \})$ as follows:

$p(V \backslash \{ \bar{v} \}) = \sum_{\bar{v}} p_V(V)$

Next, using the conditional probability expression, we know that:

$p(V \backslash \{ \tilde{v} \} | \tilde{v}) = \frac{p_V(V)}{p_{\tilde{v}}(\tilde{v})} \Rightarrow p_V(V) = p(V \backslash \{ \tilde{v} \} | \tilde{v} ) \cdot p_{\tilde{v}}(\tilde{v})$

Finally, we can rewrite this as:

$p(V \backslash \{ \bar{v} \}) = \sum_{\bar{v}} p(V \backslash \{ \bar{v} \}) p_{\tilde{v}}(\tilde{v})$

Here:

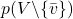$p(V \backslash \{ \bar{v} \})$ is the marginalized probability over the remaining variables.
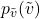$p_{\tilde{v}}(\tilde{v})$ is the marginal probability of the variable $\tilde{v}$ .

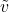This shows how the marginal probability can be written as a weighted sum of the conditional probabilities, with the weights being the marginal probabilities of the variables that were marginalized out.

Step 4: Interpreting Marginalization

The process of marginalization can be understood as computing the weighted sum of the conditional probabilities of the remaining variables, where the weights are given by the marginal probabilities of the variable being marginalized. Essentially, each possible value of $\tilde{v}$ contributes to the final marginal distribution, with its contribution weighted by its marginal probability $p_{\tilde{v}}(\tilde{v})$ .

Summary

Marginalization corresponds to computing a weighted sum of the conditional probabilities, where the weights are the marginal probabilities of the variables being marginalized.
Marginalization involves summing out a variable (or set of variables) from the joint distribution.
We can convert a joint probability into a conditional probability using the definition of conditional probability.
By combining these ideas, we can express the marginalized probability distribution in terms of conditional probabilities and the marginal probabilities of the marginalized variable.