Main Reference: https://arxiv.org/abs/2405.08793
Probabilistic Graphical Models
Probabilistic Graphical Models (PGMs) are powerful tools that represent the joint probability distribution of a set of random variables in terms of their conditional dependencies, which are typically defined by a graph structure. A fundamental task in PGMs is sampling from the joint distribution, and this can be achieved using a method known as ancestral sampling.
Key Idea
The essence of ancestral sampling is to generate samples from the joint distribution by leveraging the graph’s structure. Specifically, we exploit the chain rule of probabilities, which decomposes the joint probability into a product of conditional probabilities based on the graph’s directed edges. For a given variable, its value depends only on the values of its parent nodes, as defined by the graph.
Sampling Procedure
1. Graph Traversal Order:
- Begin with the variables with no parents (root nodes) in the graph. These variables are sampled from their marginal distributions since they are not conditioned on other variables.
- Then, proceed to sample the remaining variables in a breadth-first order (or topological order), ensuring that all parent nodes of a variable are sampled before sampling the variable itself.
2. Sampling Rule for Each Variable:
For each variable ![]() , given its parents
, given its parents ![]() , sample its value from its conditional probability distribution:
, sample its value from its conditional probability distribution:
![]()
where:
 is the sampled value of
is the sampled value of  ,
,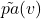 is the set of sampled values for the parent nodes of
is the set of sampled values for the parent nodes of  ,
,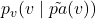 is the conditional distribution of
is the conditional distribution of  given its parent nodes.
given its parent nodes.
3. Sampling Parent Nodes:
For any node ![]() (the parents of
(the parents of ![]() ), its value
), its value ![]() is sampled using its own conditional probability distribution:
is sampled using its own conditional probability distribution:
![]()
This recursive process ensures that all necessary parent values are available before sampling any variable.
Why It Works
Ancestral sampling works because it directly follows the chain rule of probabilities:
![]()
where each term ![]() represents the conditional probability of a variable given its parents. By sampling in topological order and respecting the conditional dependencies, we ensure that the sampled values accurately represent the joint distribution.
represents the conditional probability of a variable given its parents. By sampling in topological order and respecting the conditional dependencies, we ensure that the sampled values accurately represent the joint distribution.
Advantages
- Exact Sampling:
- Ancestral sampling produces exact samples from the joint distribution without any approximation errors or bias.
- Simple Implementation:
- The method is straightforward and only requires knowledge of each node’s graph structure and conditional probability distributions.
Example
Consider a simple Bayesian Network with three variables ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() . The joint distribution is given by:
. The joint distribution is given by:
![]()
Using ancestral sampling:
- Sample
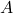 from its marginal distribution
from its marginal distribution 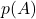 .
. - Given the sampled value of
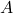 , sample
, sample 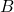 from
from 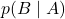 .
. - Given the sampled value of
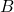 , sample
, sample 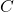 from
from 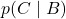 .
.
This process ensures that the sampled values ![]() are consistent with the joint distribution
are consistent with the joint distribution ![]() .
.
A Bayesian network (BN) is a probabilistic graphical model for representing knowledge about an uncertain domain where each node corresponds to a random variable and each edge represents the conditional probability for the corresponding random variables
Representing Probability Distribution
A probability distribution can be represented as a table, which consists of two columns:
- The values that the variable can take.
- The probabilities (or densities) associated with those values.
For a discrete variable ![]() , the probability table satisfies the normalization condition:
, the probability table satisfies the normalization condition:
![]()
For continuous variables, this is expressed as an integral:
![]()
Learning from Samples
If we have a set of samples ![]() drawn from an unknown distribution over a discrete variable
drawn from an unknown distribution over a discrete variable ![]() , we can approximate the original distribution using a frequency table. Each row in the table is computed as:
, we can approximate the original distribution using a frequency table. Each row in the table is computed as:
![Rendered by QuickLaTeX.com \[\left(v, \frac{1}{N} \sum_{n=1}^{N} \mathbf{1}(\tilde{v}_n = v) \right)\]](https://igorazevedo.com/blog/wp-content/ql-cache/quicklatex.com-48b6517dfc9dfb6c37b273d30845d0f6_l3.png)
where ![]() is an indicator function that equals 1 if
is an indicator function that equals 1 if ![]() and 0 otherwise.
and 0 otherwise.
Maximum Likelihood Learning
As explained above, the frequency table corresponds to maximum likelihood estimation (MLE).
In MLE, the probability of each value ![]() is estimated as the fraction of samples that take that value:
is estimated as the fraction of samples that take that value:
![Rendered by QuickLaTeX.com \[q_v(v) = \frac{1}{N} \sum_{n=1}^{N} \mathbf{1}(\tilde{v}_n = v)\]](https://igorazevedo.com/blog/wp-content/ql-cache/quicklatex.com-8aa9df14e1f25c695327ba4f10f3686c_l3.png)
While effective in large-sample scenarios, this approach has limitations:
- If
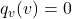 for some
for some  , this implies zero probability for values that were not observed, even if they might occur with a small but non-zero probability.
, this implies zero probability for values that were not observed, even if they might occur with a small but non-zero probability. - This limitation can be mitigated using regularization.
Conditional Probability and Regularization
The conditional probability ![]() is defined as:
is defined as:
![]()
If ![]() , the conditional probability is not well-defined. Regularization techniques can help address this by smoothing the probabilities and ensuring robustness when samples are sparse or certain values are missing.
, the conditional probability is not well-defined. Regularization techniques can help address this by smoothing the probabilities and ensuring robustness when samples are sparse or certain values are missing.
Structural Causal Models
The directed edges typically encode conditional dependencies between variables in probabilistic graphical models. However, the direction of an edge in a graph does not necessarily reflect the causal relationship between variables.
From a probabilistic standpoint, the joint distribution remains unchanged if the direction of the edges is flipped. This is formalized using Bayes’ rule:
![]()
This equation implies that we can “flip” the arrow of an edge between variables ![]() and
and ![]() without altering the joint or conditional probabilities. While this property simplifies probabilistic inference, it raises challenges when using graphical models to infer causal relationships.
without altering the joint or conditional probabilities. While this property simplifies probabilistic inference, it raises challenges when using graphical models to infer causal relationships.
Addressing the Confusion in Causal Inference
We adopt a different representation of the generative process underlying the probabilistic graphical model to clarify causal relationships.
Instead of focusing purely on the probabilistic distribution, we describe the process of generating a value for each variable ![]() as a deterministic function of:
as a deterministic function of:
- Its parent nodes
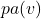 ,
, - An additional external (exogenous) noise variable
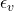 .
.
This is expressed as:
![]()
Here:
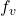 is a deterministic function specific to
is a deterministic function specific to  ,
,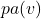 are the parent variables of
are the parent variables of  ,
,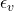 is an independent noise variable that captures randomness.
is an independent noise variable that captures randomness.
This formulation explicitly separates deterministic relationships (via ![]() ) and randomness (via
) and randomness (via ![]() ), providing a clearer framework for causal reasoning.
), providing a clearer framework for causal reasoning.
Why Structural Causal Models Are More Informative
The deterministic function ![]() makes the underlying generative process explicit:
makes the underlying generative process explicit:
- Perturbation Insight:
- Changing
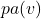 or
or 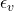 affects
affects  , enabling us to reason how
, enabling us to reason how  would change under different conditions.
would change under different conditions.
- Changing
- Causal Interventions:
- Intervening on
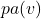 allows us to study cause-and-effect relationships systematically.
allows us to study cause-and-effect relationships systematically.
- Intervening on
Example: Pushing a Book
Imagine pushing a book on your desk with a force ![]() .
.
The resulting position of the book, ![]() , depends deterministically on:
, depends deterministically on:
- The applied force
 , representing
, representing 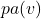 .
. - Unknown noise factors
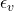 , such as desk friction.
, such as desk friction.
By modifying ![]() (the force applied), we can predict the new position
(the force applied), we can predict the new position ![]() while accounting for the stochastic nature of
while accounting for the stochastic nature of ![]() . This ability to isolate and analyze specific causal influences is central to Structural Causal Models (SCMs).
. This ability to isolate and analyze specific causal influences is central to Structural Causal Models (SCMs).
Structural Causal Models as Triplets
A Structural Causal Model (SCM) is defined by the triplet:
![]()
where:
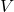 is the set of variables,
is the set of variables,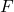 is the set of deterministic functions
is the set of deterministic functions 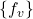 ,
, is the set of noise variables
is the set of noise variables 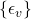 .
.
This contrasts with probabilistic graphical models, which emphasize joint distributions. SCMs focus on the mechanisms generating those distributions.
Converting SCMs to Probabilistic Graphical Models
SCMs can be converted into probabilistic graphical models using a change of variables approach:
- Assume a known prior distribution over
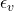 ,
, - Transform the noise variables into values for
 using the functions
using the functions 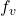 :
:
![]()
As discussed earlier, this allows sampling from the joint distribution or performing ancestral sampling.
Once we have an SCM, we can use it for various tasks, including inference and reasoning. For example, we can answer questions about the underlying causal structure by sampling from the joint distribution.
Counterfactual Reasoning
One of the key strengths of SCMs is their ability to support counterfactual reasoning:
- Counterfactuals allow us to ask:
- “What would have happened if some variables were set differently?”
- For example, if a target variable
 had a different value, what noise factors (
had a different value, what noise factors (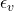 ) would explain that change?
) would explain that change?
Posterior Over Noise Variables
To answer counterfactual questions, we compute the posterior distribution over the noise variables ![]() , conditioned on observed configurations of
, conditioned on observed configurations of ![]() and its parents. The posterior distribution is denoted as:
and its parents. The posterior distribution is denoted as:
![]()
where ![]() corresponds to the set of all
corresponds to the set of all ![]() values consistent with the observed configuration of
values consistent with the observed configuration of ![]() .
.
Practical Implication
By using SCMs, we can:
- Fix certain variables in
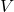 to specific values (interventions),
to specific values (interventions), - Allow the external noise variables
 to vary according to
to vary according to 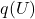 ,
, - Study how these interventions propagate through the system, enabling us to answer “what if” questions about alternative scenarios.
Summary
- Probabilistic graphical models encode dependencies but are agnostic to causal relationships.
- Structural causal models introduce deterministic functions
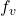 and noise variables
and noise variables 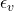 , enabling explicit modeling of causal processes.
, enabling explicit modeling of causal processes. - SCMs are particularly powerful for counterfactual reasoning, systematically answering “what would have happened if” scenarios.
